基于源代码的RRA算法原理解析
基于源代码的RRA算法原理解析
使用RRA算法做基因表达meta分析的文章很多，基于某个好友博士答辩中涉及到此方法，需要对该算法深入解析，顺道抽空研究了一下（主要是实在看不下去文章直译牛头不对马嘴。。。。。他翻译如下）：
从源码如上一步一步解析如下：
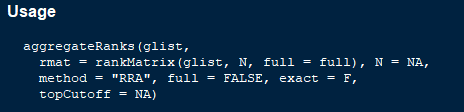
看代码很简单，就一个函数，查看此函数源码，核心如下:
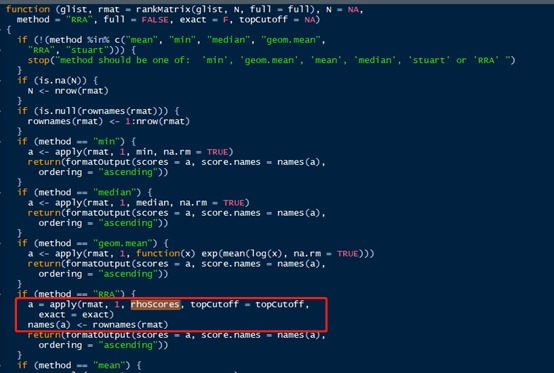
关键点在于红色框处的代码，红色框处的意思其实就是按rmat矩阵的每一行进行代入rhoScores函数，计算最终的一个值，那么rmat矩阵是什么呢，他是一个行为基因列为每个比较组的foldchange的矩阵
比如我们有三套数据A、B、C,每套数据都做了差异分析，得到了一个差异基因列表，从按照差异大小进行排序比如：
A: "e"
"p" "x" "w"
B："l" "x" "i"
"s" "k" "w" "u" "n"
"e" "y"
C:"e" "j" "t" "o" "x"
"l" "z" "m" "a" "y"
"n" "q"
我们首先统计这三组数据集中总共包含哪些基因（即取并集并去重复）,共有18个，那么我们接下来就可以构建18*3这样的矩阵了，内容怎么填呢，就拿A来说有4个基因排序为e=1，p=2，x=3，w=4;而基因组中所有基因共有N个(假如我们这里背景基因共26个)，所以e对应的值为1/26=0.03846，p对应的值为2/26=0.0769，以此类推四个基因全部计算完，剩下的不在A的差异列表中的则归为1，对于B、C组样本类似的计算；最终就得到了这样的一个标准化的秩向量矩阵了，在原文中的描述是这样的：
建立矩阵之后如：
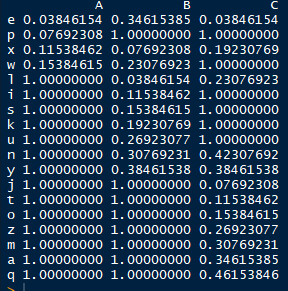
计算完归一化的秩向量矩阵之后，进一步的计算每个基因的在A、B、C三组中的归一化后的秩得分，比如基因e的秩得分为0.03846154,0.34615385,0.03846154;首先根据基因e的在秩得分从大到小排序，依次对于每一个排序后的得分分别生成一个β分布（形状参数为排序的秩次和倒秩），计算该得分下对应的累计概率。
Beta分布是一个定义在[0,1]区间上的连续概率分布族，它有两个正值参数，称为形状参数，一般用\alphaα和\betaβ表示。
最终我们得到了基因e对应的三组样本中的秩次发生的概率，我们选择概率最小的那个作为基因e的发生概率，再进一步的乘以样本的组别数目即乘以3，最终得到了基因e的RRA得分（当该得分大于1时则让其等于1）。
依次分别计算每一个基因的得分最终得分如下
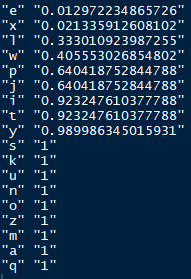
以上即整个RRA算法的实现过程。
- 发表于 2019-02-15 21:36
- 阅读 ( 9076 )
- 分类：编程语言
