这篇文章详细介绍了 PCA、tSNE、UMAP，原始链接为：https://blog.csdn.net/qq_43337249/article/details/116612811 ，以下为备份

常见的降维方法基本原理及代码实例

0.前言：什么时候要降维聚类？降维目的-方法概述

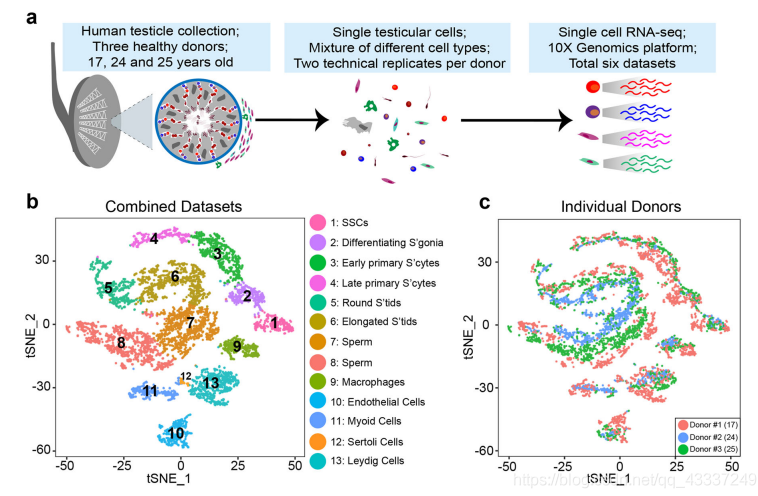
在开始回答这个问题前，我们看一下降维分析的应用，上图来自发表在2018年Cell Research（IF>20）上的一篇文章
《The adult human testis transcriptional cell atlas》，作者通过降维对donor细胞类群进行评估，
发现他们能够较好的叠加（具有同质性），又通过`tSNE`对细胞进行`降维聚类`，共有13个细胞亚群,很好地展示了亚群分类结果

在实际的机器学习项目中，特征选择/降维是必须进行的，因为在数据中存在以下几个 方面的问题：

1.数据的多重共线性：特征属性之间存在着相互关联关系。多重共线性会导致解的空间不稳定， 从而导致模型的泛化能力弱；

2.高纬空间样本具有稀疏性，导致模型比较难找到数据特征；过多的变量会妨碍模型查找规律；

3.仅仅考虑单个变量对于目标属性的影响可能忽略变量之间的潜在关系。

那么降维的目的是什么？

通过特征选择/降维的目的是：

1.减少特征属性的个数，确保特征属性之间是相互独立的

2.解决特征矩阵过大， 导致计算量比较大，训练时间长的问题，便于发现规律

一位博主总结了大家常见的问题：（参考原文链接：https://blog.csdn.net/weixin_43612049/article/details/101794520）

问题一：什么是降维？

降维是指通过保留一些比较重要的特征，去除一些冗余的特征，减少数据特征的维度。而特征的重要性取决于该特征能够表达多少数据集的信息，也取决于使用什么方法进行降维。一般情况会先使用线性的降维方法再使用非线性的降维方法，通过结果去判断哪种方法比较合适。

问题二：在哪里用到降维？

1）特征维度过大，可能会导致过拟合时

2）某些样本数据不足的情况（缺失值很多）

3）特征间的相关性比较大时

问题三：降维的好处？

（1）节省存储空间；

（2）加速计算速度，维度越少，计算量越少，并且能够使用那些不适合于高维度的算法；

（3）去除一些冗余的特征（原数据中既有平方米和平方英里的特征–即相关性大的特征）

（4）便于观察和挖掘信息（如将数据维度降到2维或者3维使之能可视化）

（5）特征太多或者太复杂会使得模型过拟合。

实现高维数据可视化的理论基础是基于降维算法。降维算法一般分为两类:
1.寻求在数据中保存距离结构的:PCA、MDS等算法
2倾向于保存局部距离而不是全局距离的。`t-SNE`  diffusion maps(UMAP)
下面我们对这些方法的原理进行介绍，并在此基础上采取iris经典数据集进行绘制图

1.PCA（主成分分析）

 1.1PCA概念

PCA 分析(Principal Component Analysis)，即主成分分析，是一种对数据进行简化分析的技术，这种方法可以有效的找出数据中最“主要”的元素和结构，去除噪音和冗余，将原有的复杂数据降维，揭示隐藏在复杂数据背后的简单结构。

PCA(Principal Component Analysis)，即主成分分析方法，是一种使用最广泛的数据降维算法。
PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。
PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的。

可以看到下图中，原本不同维度（Gene）经过正交特征提取后，变为2维，便于我们更好地观测结果，注意新构建的特征是在原本特征的基础上构建的，包含其主要信息

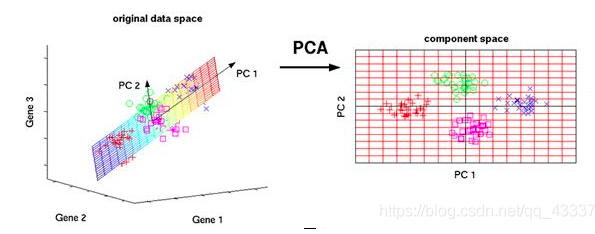
PCA是将数据的最主要成分提取出来代替原始数据，也就是将n维特征映射到新的维度中，由k维正交特征组成的特征空间就是主成分，使用的降维方法就是投影。

问题是怎样抽取数据的主要成分，如何衡量投影后保存的信息呢？PCA算法使用方差来度量信息量，为了确保降维后的低维度数据尽可能多的保留原始数据的有效信息，需要使降维后的数据尽可能的分散，从方差角度理解就是保留最大的方差。那么如何得到包含最大差异性的主成分呢？实际上，计算数据矩阵的协方差矩阵，得到协方差矩阵的特征值和特征向量，然后选择特征值最大的k个特征对应的特征向量组成的矩阵，就将原始数据矩阵投影到了新的k维特征空间，实现了数据特征的降维。

1.2 PCA代码实例

#使用经典iris数据集，df读入前四列
df <- iris[1:4]
#查看数据的结构，head查看前5行，tail查看后6行
head(df，5)
tail(df,6) 
##======================= Caculate the principal components（计算主成分）
##prcomp的功能是计算PCA
df_pca <-prcomp(df)
str(df_pca)  #可以查看数据结构
df_pcs  <-data.frame(df_pca$x,Species = iris$Species)
head(df_pcs,10)   #查看前10行主成分结果
##======================= ggplot2包进行绘图
library(ggplot2)
library(tidyverse)
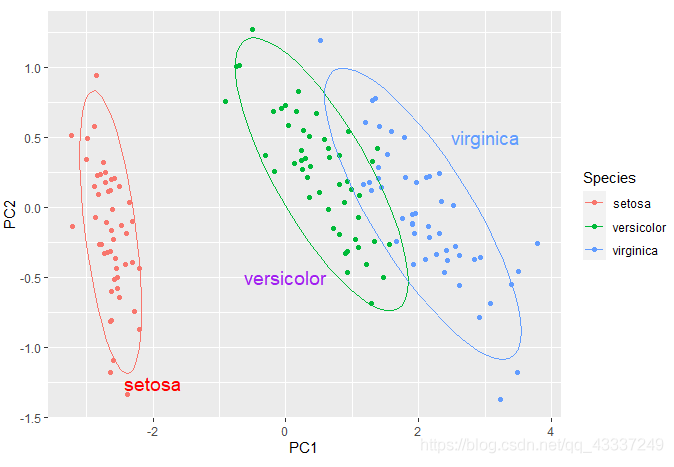
ggplot(df_pcs,aes(x=PC1,y=PC2,color=Species))+
  geom_point()
#去掉背景及网格线
ggplot(df_pcs,aes(x=PC1,y=PC2,color=Species))+
geom_point()+
  stat_ellipse(level = 0.95, show.legend = T) + 
  annotate('text', label = 'setosa', x = -2, y = -1.25, size = 5, colour = 'red') +
  annotate('text', label = 'versicolor', x = 0, y = - 0.5, size = 5, colour = '#00ba38') +
  annotate('text', label = 'virginica', x = 3, y = 0.5, size = 5, colour = '#619cff')
theme_bw()+
theme(panel.border=element_blank(),panel.grid.major=element_blank(),
      panel.grid.minor=element_blank(),axis.line= element_line(colour = "blue"))

结果：

2.tSNE

2.1 tSNE概念

关键词：

1.t分布-随机邻近嵌入 
2.相似度转化为条件概率
3.学生t分布

1.`t-SNE 算法概述`

t-SNE （全称为 t-distributed Stochastic Neighbor Embedding，翻译为 t分布-随机邻近嵌入）是通过将数据点之间的相似度转化为条件概率，原始空间中数据点的相似度由高斯联合分布表示，嵌入空间中数据点的相似度由学生t分布 表示 能够将高维空间中的数据映射到低维空间中，并保留数据集的局部特性。

2.`t-SNE原理`

t-SNE本质是一种嵌入模型，主要用于高维数据的降维和可视化。

如果想象在一个三维的球里面有均匀分布的点，不难想象，如果把这些点投影到一个二维的圆上一定会有很多点是重合的。

所以，为了在二维的圆上想尽可能表达出三维里的点的信息，大神Hinton采取的方法：

把由于投影所重合的点用不同的距离（差别很小）表示。

这样就会占用原来在那些距离上的点，原来那些点会被赶到更远一点的地方。

t分布是长尾的，意味着距离更远的点依然能给出和高斯分布下距离小的点相同的概率值。

从而达到高维空间和低维空间对应的点概率相同的目的。

参考文献：

1.https://cloud.tencent.com/developer/article/1549992

2.http://www.360doc.com/content/19/0403/11/51784026_826128783.shtml

3.UMAP

## 3.1UMAP概念

对高维单细胞数据的可视化展示，以t-SNE为代表的非线性降维技术，由于其能够避免集群表示的过度拥挤，在重叠区域上能表示出不同的集群而被广泛运用。然而，任何技术方法都不是完美的，t-SNE也一样，它的局限性体现在丢失大规模信息(集群间关系)、计算时间较慢以及无法有效地表示非常大的数据集]等方面。

那么，有没有其它方法能在一定程度上克服这些弱点呢？

UMAP就是这样一个能解决这些问题的降维和可视化的工具。

UMAP：统一流形逼近与投影(UMAP，Uniform Manifold Approximation and Projection)是一种新的降维流形学习

技术。UMAP是建立在黎曼几何和代数拓扑理论框架上的。UMAP是一种非常有效的可视化和可伸缩降维算法。在可视化

质量方面，UMAP算法与t-SNE具有竞争优势，但是它保留了更多全局结构、具有优越的运行性能、更好的可扩展性。

此外，UMAP对嵌入维数没有计算限制，这使得它可以作为机器学习的通用维数约简技术。

t-SNE和UMAP、PCA的应用比较：

1.小数据集中，t-SNE和UMAP差别不是很大

2.大数据集中，UMAP优势明显（30多万个细胞的降维可视化分析）

3.通过数据降维和可视化展示的比较显示，PCA分群效果最差，UMAP和t-SNE都成功将与相似细胞群相对应的簇聚集在一起。

4.与t-SNE相比，UMAP还提供了有用的和直观的特性、保留了更多的全局结构，特别是细胞子集的连续性。

参考文章：单细胞数据降维可视化：https://www.bio-equip.com/showarticle.asp?id=453107027